二维凸包
前言
二维凸包。但是笔者学的依托答辩。
算法讲解
定义
首先来了解什么是二维凸包。
对于一个集合D,D中任意有限个点的凸组合的全体称为D的凸包。
或:
对于一个集合D,所有包含D的凸集之交称为D的凸包。
————某个经常出锅的百科
其实通俗地来讲,凸包就是把一个点集最外面的点连接起来构成的 凸多边形,且能够包含所有点。
还有一种描述方法:凸包是指覆盖平面上n个点的最小的凸多边形。
算法
每一种模板都有很多种人类智慧做法。那接下来将由浅入深地介绍几种求凸包地算法。
斜率逼近法
其实算是一种比较好想的思路了。
- 首先在所有点中找出来一个 $y$ 值最小的点,记为 $P_i$。
- 从 $P_i$ 开始,然后逆时针找与 $P_i$ 相连的边斜率 $k(k>0)$ 最小的点(如果有多个符合条件的点,则取最远的那个)。
- 从选出来的 $p_i$ 开始不断重复(2)的方法,直到找到 $m$ 使得 $P_m=P_1$。
时间复杂度 $O(nm)$($n$ 为点的个数,$m$ 为凸包上的点的数量)。
但是一旦凸包上的两个点之间的斜率趋于无限大(即几乎和 y 轴平行),还是有局限性。
那么就有新的算法了。
Jarvis 算法
本质上还是数学构造法。
针对于斜率逼近法的缺陷,可以做出一些改进:
把斜率逼近法(2)步骤中的斜率改为极角,每次选择极角最小的那个点加入凸包,然后从选出来的这个点继续重复此步骤(如果有极角相同的,则选择最远的那个点)。
时间复杂度 $O(nm)$,除了时间复杂度外无明显的缺陷,但是就是这个时间复杂度的缺陷令我们无法接受…
Graham 算法
本质:
Graham 算法维护一个凸壳,通过不断在 凸壳(就是凸包的一部分)中加入新的点和去除影响凸性的点,最后形成 凸包。
该算法主要由两部分组成:
- 排序
- 扫描
排序
选择所有点中 $y$ 值最小的点,标记为 $P_1$。
然后在剩下的点中按照极角的大小逆时针排序(求极角的函数:atan2(p.x,p.y)),编号为 $P_2\sim n$。
加入凸包
按照排序的顺序枚举每一个点,依次连线,考虑将当前的点加入栈中进行处理:
- 如果新加入的点与栈顶元素的连线影响了栈中凸包的凸性的话,就弹出栈顶元素。
- 一直重复以上步骤,最后把当前元素加入栈中。
这个的正确性可以手玩一下,扫描的复杂度也是 $O(n)$。但是显然不可能这么完美。算上排序的时间复杂度 $O(n\log_n)$,总的时间复杂度为 $O(n\log_n)$。
下面放一下 洛谷二维凸包模板。Code1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
using namespace std;
const int N = 1e5 + 10;
const double eps = 1e-6;
int n;
int cnt = 0;
double sum = 0.0;
struct point {
double x, y;
point (const double& x0 = 0, const double& y0 = 0) : x(x0), y(y0) { }
point operator + (const point& t) const {
return point(x + t.x, y + t.y);
}
point operator - (const point& t) const {
return point(x - t.x, y - t.y);
}
point operator * (const double& t) const {
return point(x * t, y * t);
}
point operator / (const double& t) const {
return point(x / t, y / t);
}
point rotate() {
return point(y, -x);
}
} p[N], low, q[N];
double dot(const point& a, const point& b) {
return a.x * b.x + a.y * b.y;
}
double cross(const point& a, const point& b) {
return a.x * b.y - a.y * b.x;
}
double len(const point& a) {
return sqrt(dot(a, a));
}
double dis(const point &a, const point &b) {
return sqrt(dot(a - b, a - b));
}
template<class T>
inline void read(T &x) {
T res = 0, f = 1; char cc = getchar();
while(! isdigit(cc)) {
if(cc == '-') f = -1;
cc = getchar();
}
while(isdigit(cc)) res = (res << 1) + (res << 3) + cc - 48, cc = getchar();
x = res * f; return ;
}
template<class T, class ...T1>
inline void read(T &x, T1 &...x1) {
read(x), read(x1...); return ;
}
template<class T>
inline void write(T x) {
if(x < 0) x = -x, put('-');
if(x > 9) write(x / 10);
put(x % 10 + 48); return ;
}
template<>
inline void write(char x) {
put(x); return ;
}
template<class T, class ...T1>
inline void write(T x, T1 ...x1) {
write(x),write(x1...); return ;
}
template <class T>
inline bool chkmax(T &x, T y) {
return x < y ? x = y , 1 : 0;
}
int sign(double a) {
if(fabs(a) < eps)
return 0;
return a > 0 ? 1 : -1;
}
bool cmp(point a, point b) {
if(sign(cross(a - low, b - low)) > 0)
return true;
if(sign(cross(a - low, b - low)) == 0 && sign(dis(low, a) - dis(low, b)) < 0)
return true;
return false;
}
bool check(point a, point b, point c) {
return sign(cross(b - a, c - b)) <= 0;
}
signed main()
{
// freopen(".in", "r", stdin);
// freopen(".out", "w", stdout);
read(n), low.y = 1e6;
for(int i = 1; i <= n; ++ i)
scanf("%lf%lf", &p[i].x, &p[i].y),
low = (sign(p[i].y - low.y) < 0 || (sign(p[i].y - low.y) == 0 && sign(p[i].x - low.x) < 0)) ? p[i] : low;
sort(p + 1, p + n + 1, cmp);
q[++ cnt] = low;
for(int i = 1; i <= n; ++ i)
{
if(sign(p[i].x - low.x) == 0 && sign(p[i].y - low.y) == 0)
continue;
while(cnt > 1 && check(q[cnt - 1], q[cnt], p[i]))
-- cnt;
q[++ cnt] = p[i];
}
q[++ cnt] = q[1];
for(int i = 1; i < cnt; ++ i)
sum += dis(q[i], q[i + 1]);
printf("%.2lf", sum);
return 0;
}
Andrew 算法
- 首先按照横坐标 $x$ 排序,易知最左边和最右边的点都在凸包上。
- 从第一个点开始遍历,用类似 Graham 算法中的方法往栈中加入新的点,形成下凸壳。
- 但是我们发现,这样扫描过去只能形成一半的凸包,即下凸壳。那我们就反过来维护,再形成上凸壳。
扫描的时间复杂度:$O(n)$,排序复杂度:$O(n\log_n)$,那总的时间复杂度:$O(n\log_n)$。
(因为懒得自己打,随便从网上贺了一篇代码)。Code1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35double cross(point A, point B)
{
return A.x * B.y - A.y * B.x;
}
double side(point a, point b, point p)
{
point A = point(b.x - a.x, b.y - a.y);
point B = point(p.x - a.x, p.y - a.y);
return cross(A, B);
}
int Andrew(int top)
{
sort(p + 1, p + n + 1);
if(n < 3)
{
puts("-1");
return;
}
st[0] = p[1], st[1] = p[2];
top = 1;
for (int i = 3; i <=n ; ++ i)//下凸包
{
while(top && side(st[top - 1], st[top], p[i]) <= 0)
-- top;
st[++ top] = p[i];
}
st[++ top] = p[n - 1];
for(int i = n - 2; i >= 1; -- i)//上凸包
{
while(top && side(st[top - 1], st[top], p[i]) <= 0)
-- top;
st[++ top] = p[i];
}
return top;
}
例题
P2742 [USACO5.1] 圈奶牛Fencing the Cows /【模板】二维凸包
模板题,没什么好说的,代码上面就有。
P3829 [SHOI2012] 信用卡凸包
links,一道很典的例题。把题目转化一下:
先不管圆弧部分,那最终的凸包所有的直线部分即为下图绿色部分: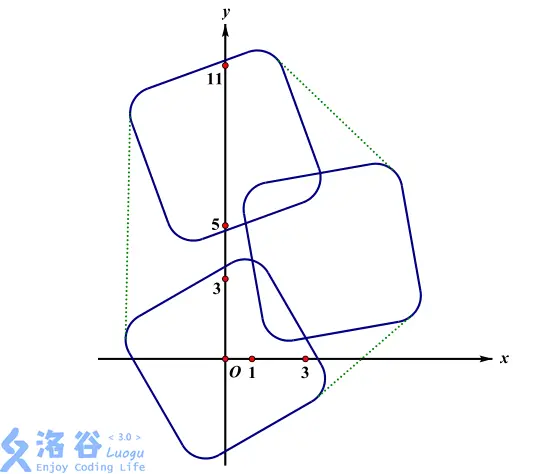
将其平移到圆心(矩形顶点)后发现:绿色部分就是所有矩形的顶点构成的凸包: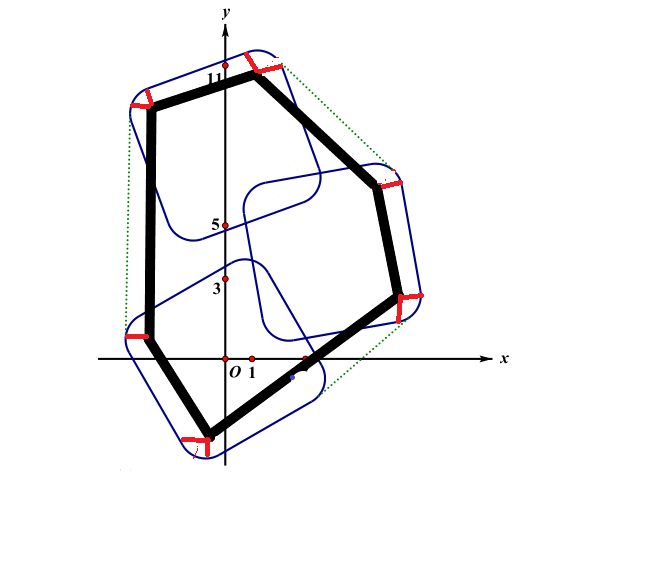
那么对所有的顶点求一个凸包即可。至于圆弧部分,所有的圆弧相加是一个完整的圆,计算即可。
1 |
|
尾声
完了,其他的自己看吧。(