向量

前言

针对尚且不清楚向量的笔者这种水平零基础讲解，限于平面几何，立体暂不做讨论。

正文

定义

相对于标量来说，向量是有方向的。例：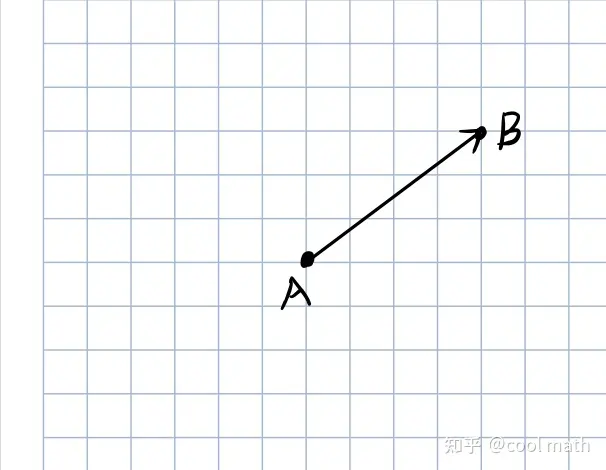

上图表示以 A 为起点，B 为终点的向量 $\overrightarrow{ab}$。
向量的大小（即长度）$|\overrightarrow{ab}|$ 称为向量的模（模长）。
定义两个向量相等：当且仅当两个向量大小相等，方向一致（不能相反），记作 $\overrightarrow{a}=\overrightarrow{b}$。
所以向量可以在坐标系内任意平移，与位置无关。

特殊向量

零向量：长度为 0 的向量，记作 $\overrightarrow{0}$，方向可以为任意方向，与任何向量共线或平行。
单位向量：长度为 1 的向量，记作 $\overrightarrow{e}$。

向量的平行与共线的形象理解

即方向相同或相反的向量，记作 $\overrightarrow{a}//\overrightarrow{b}$。

向量加法

向量加法遵从三角形法则。即：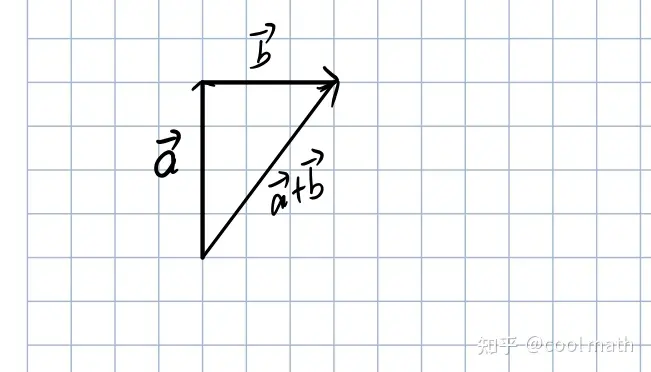

也遵从平行四边形法则，即：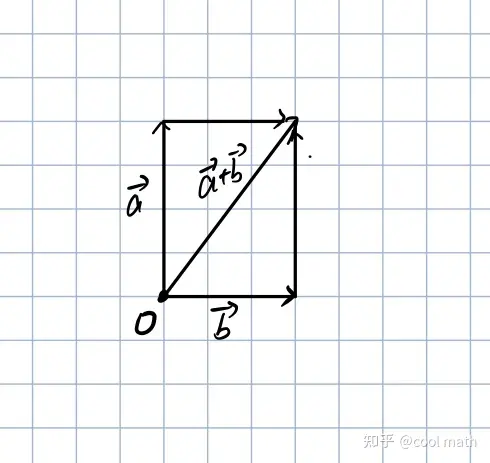

那么，$\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{BC}$。
且向量的加法满足交换律、结合律和交换律。
根据三角形法则：
$|\overrightarrow{a}+\overrightarrow{b}|\leq |\overrightarrow{a}|+|\overrightarrow{b}|$。

相反变量

长度相同，方向相反的变量；$\overrightarrow{AB}=-\overrightarrow{BA}$。

向量减法

那么，$\overrightarrow{a}-\overrightarrow{b}=\overrightarrow{a}+(\overrightarrow{-b})$.
$\overrightarrow{AB}-\overrightarrow{AC}=\overrightarrow{CB}$：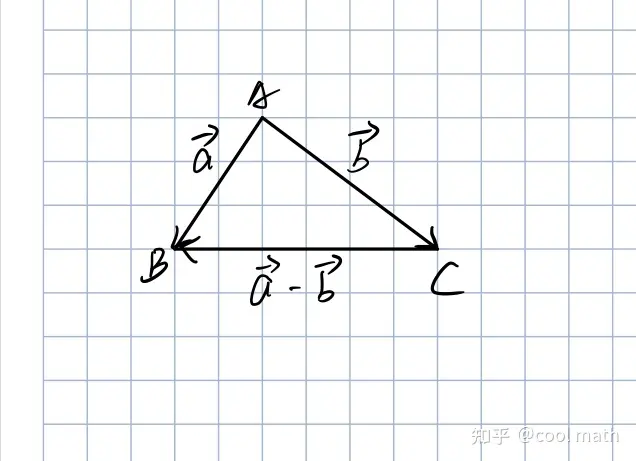

向量夹角

将 $a$ 和 $b$ 平移到一个初始点，之间的夹角称为 $a$ 和 $b$ 的夹角，可以称之为 $\theta$。
$\theta =0$ 时，两个向量同向。
$\theta =\frac{\pi}{2}$ 时，两个向量垂直。
$\theta =\pi$ 时，两个向量反向。

向量乘法

数乘

定义

相当于向量的放缩，运算结果仍为向量。例：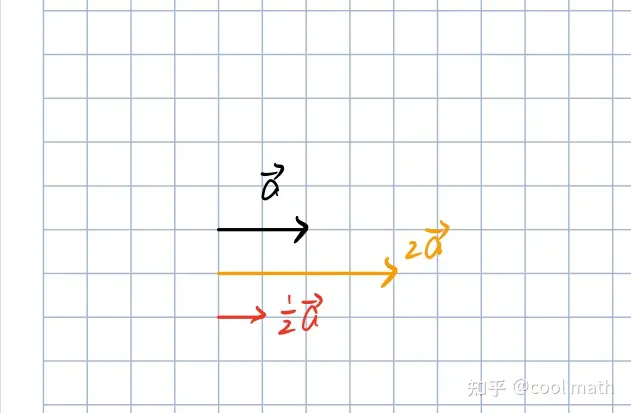

性质

1. $|\gamma \overrightarrow{a}|=|\gamma| |\overrightarrow{a}|$。
2. $\gamma>0$ 时，$\gamma\overrightarrow{a}$ 与 $\overrightarrow{a}$ 同向；$\gamma<0$ 时，两者反向。
3. 满足交换律、结合律和分配率。

共线的定义

向量 $\overrightarrow{a}(a\ne \overrightarrow{0})$ 与 $\overrightarrow{b}$ 共线的充要条件为：存在唯一一个实数 $\gamma$ 使得 $\gamma \overrightarrow{a}=\overrightarrow{a}$。

内积

定义

$\overrightarrow{a}\cdot \overrightarrow{b}=|\overrightarrow{a}| |\overrightarrow{b}| \cos\theta$，又称点乘（点积），结果为标量。满足交换律、结合律和分配律。
那么就可以用 $\cos\theta=\frac{\overrightarrow{a}\cdot\overrightarrow{b}}{|\overrightarrow{a}||\overrightarrow{b}|}$ 来方便的计算夹角。

几何意义

一个向量在另一个向量上的投影长度与后者的模长乘积。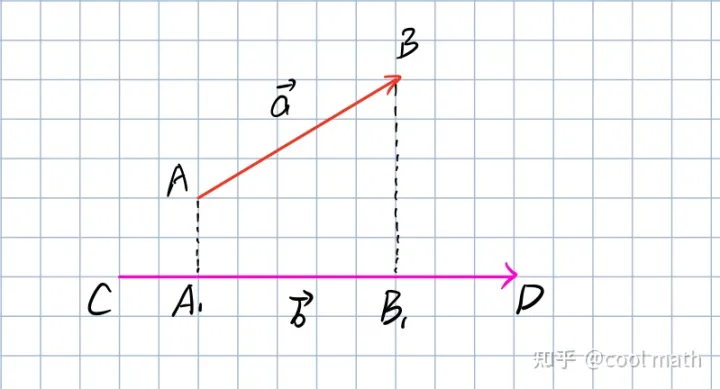

外积（二维）

定义

$\overrightarrow{a}\times\overrightarrow{b}=|\overrightarrow{a}||\overrightarrow{b}|\sin\theta$，又称叉乘（叉积），结果为向量。两个向量的外积与这两个向量所在的平面垂直（右手定则），也称作法向量：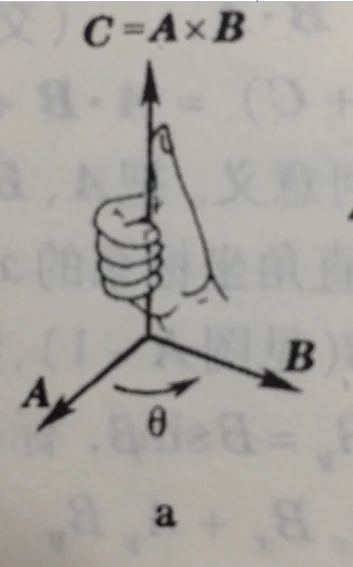

外积模长等于两个向量组成的平行四边形面积（但是是有向面积，可这样理解：如果 $\overrightarrow{a}$ 逆时针转向 $\overrightarrow{b}$，结果为正，否则为负）

性质

1. $\overrightarrow{a}\times\overrightarrow{a}=0$
2. $\overrightarrow{a}\times\overrightarrow{b}=-\overrightarrow{a}\times\overrightarrow{b}$（不满足交换律）。
3. $\overrightarrow{a}\times(\overrightarrow{b}+\overrightarrow{c})=\overrightarrow{a}\times\overrightarrow{b}+\overrightarrow{a}\times\overrightarrow{c}$（满足结合律）。

向量的平面直角坐标系表示法

因为前文提到过，向量可以任意平移，如果我们把向量的起点移动到坐标原点，那么平面上的一个个点 $(x,y)$ 就可以表示向量，表示方向为 $(0,0)$ 到 $(x,y)$、大小为 $\sqrt{x^2+y^2}$ 的向量（一一对应关系）。
这样的话前文所述很多公式都可以转化，将 $\overrightarrow{a}$ 与 $\overrightarrow{b}$ 分别用 $(x_1,y_1)$ 与 $(x_2,y_2)$ 表示。
总之就非常的优美。

向量加法

$\overrightarrow{a}+\overrightarrow{b}=(x_a+x_b,y_a+y_b)$

向量数乘

$\overrightarrow{a}\gamma=(x\gamma,y\gamma)$

向量内积

$\overrightarrow{a}\cdot\overrightarrow{b}=x_ax_b+y_ay_b$

向量外积

$|\overrightarrow{a}\times\overrightarrow{b}|=x_ay_b-x_by_a$

向量旋转

这个前文并没有提到过，但是手玩一下还是很好推的。$\overrightarrow{a}$ 绕原点逆时针旋转 $\theta$：
$(x\cos\theta-y\sin\theta,x\sin\theta+y\cos\theta)$

尾声

向量篇告一段落，其他的应用最好自己手玩，考场上推完全来的及。（其实就是懒得写了）